Geometry

The Elements ( Stoicheia) is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt c. 300 BC. It is a collection of definitions, postulates, propositions (theorems and constructions), and mathematical proofs of the propositions. The books cover plane and solid Euclidean geometry, elementary number theory, and incommensurable lines. Elements is the oldest extant large-scale deductive treatment of mathematics. It has proven instrumental in the development of logic and modern science, and its logical rigor was not surpassed until the 19th century.

Euclid's Elements has been referred to as the most successful and influential textbook ever written. It was one of the very earliest mathematical works to be printed after the invention of the printing press and has been estimated to be second only to the Bible in the number of editions published since the first printing in 1482, with the number reaching well over one thousand. For centuries, when the quadrivium was included in the curriculum of all university students, knowledge of at least part of Euclid's Elements was required of all students. Not until the 20th century, by which time its content was universally taught through other school textbooks, did it cease to be considered something all educated people had read.

Let it be granted

1. That a straight line may be drawn from any one point to any other point:

2. That a terminated straight line may be produced to any length in a straight line:

3. And that a circle may be described from any centre, at any distance from that centre.

AXIOMS

1. Things which are equal to the same thing are equal to one another.

2. If equals be added to equals the wholes are equal.

3. If equals be taken from equals the remainders are equal.

4. If equals be added to unequals the wholes are unequal.

5. If equals be taken from unequals the remainders are unequal.

6. Things which are double of the same thing are equal to one another.

7. Things which are halves of the same thing are equal to one another.

8. Magnitudes which coincide with one another, that is, which exactly fill the same space, are equal to one another.

9. The whole is greater than its part.

10. Two straight lines cannot enclose a space.

11. All right angles are equal to one another.

12. If a straight line meet two straight lines, so as to make the two interior angles on the same side of it taken together less than two right angles, these straight lines, being continually produced, shall at length meet on that side on which are the angles which are less than two right angles.

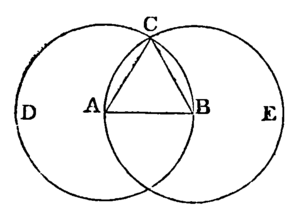
PROPOSITION 1. PROBLEM.

To describe an equilateral triangle on a given finite straight line.

Let AB be the given straight line; it is required to describe an equilateral triangle on AB.

From the centre A at the distance AB describe the circle BCD. [Postulate 3.

From the centre B, at the distance BA, describe the circle ACE. [Postulate 3.

From the point C, at which the circles cut one another, draw the straight lines CA and CB to the points A and B. [Post. 1.

ABC shall be an equilateral triangle.

Because the point A is the centre of the circle BCD, AC is equal to AB. [Definition 15.

And because the point B is the centre of the circle ACE, BC is equal to BA. [Definition 15.

But it has been shewn that CA is equal to AB;

therefore CA and CB are each of them equal to AB.

But things which are equal to the same thing are equal to one another. [Axiom 1.

Therefore CA is equal to CB.

Therefore CA, AB, BC are equal to one another.

Wherefore the triangle ABC is equilateral, [Def. 24. and it is described on the given straight line AB. Q.E.F.

PROPOSITION 2. PROBLEM.

From a given point to draw a straight line equal to a given straight line.

Let A be the given point, and BC the given straight line: it is required to draw from the point A a straight line equal to BC.

From the point A to B draw the straight line AB; [Post. 1.
and on it describe the equilateral triangle DAB, [I. 1.
and produce the straight lines DA, DB to E and F. [Post. 2.
From the centre B, at the distance BC, describe the circle CGH, meeting DF at G. [Post. 3.
From the centre D, at the distance DG, describe the circle GKL, meeting DE at L. [Post. 3.
AL shall be equal to BC.

Because the point B is the centre of the circle CGH, BC is equal to BG. [Definition 15.
And because the point D is the centre of the circle GKL, DL is equal to DG; [Definition 15.
and DA, DB parts of them are equal; [Definition 24.
therefore the remainder AL is equal to the remainder BG. [Axiom 3.
But it has been shewn that BC is equal to BG;
therefore AL and BC are each of them equal to BG.
But things which are equal to the same thing are equal to one another. [Axiom 1.
Therefore AL is equal to BC.

Wherefore from the given point A a straight line AL has been drawn equal to the given straight line BC. q.e.f.

PROPOSITION 3. PROBLEM

From the greater of two given straight lines to cut off a part equal to the less.

Let AB and C be the two given straight lines, of which

AB is the greater: it is required to cut off from AB the greater, a part equal to C the less.

From the point A draw the straight line AD equal to C; [I. 2.
and from the centre A, at the distance AD, describe the circle DEF meeting AB at E. [Postulate 3.
AE shall be equal to C.

Because the point A is the centre of the circle DEF, AE is equal to AD. [Definition 15.
But C is equal to AD. [Construction.
Therefore AE and C are each of them equal to AD.
Therefore AE is equal to C. [Axiom 1.

Wherefore from AB the greater of two given straight lines a part AE has been cut off equal to C the less. q.e.f.

PROPOSITION 4. THEOREM

If two triangles have two sides of the one equal to two sides of the other, each to each, and have also the angles contained by those sides equal to one another, they shall also have their bases or third sides equal; and the two triangles shall be equal, and their other angles shall be equal, each to each, namely those to which the equal sides are opposite.

Let ABC, DEF be two triangles which have the two sides AB, AC equal to the two sides DE, DF, each to each, namely, AB to DE, and AC to DF, and the angle BAC equal to the angle EDF: the base BC shall be equal to the base EF, and the triangle ABC to the triangle DEF, and the other angles shall be equal, each to each, to which the equal sides are opposite, namely, the angle ABC to the angle DEF, and the angle ACB to the angle DFE.

For if the triangle ABC be applied to the triangle DEF, so that the point A may be on the point D, and the straight line AB on the straight line DE, the point B will coincide with the point E, because AB is equal to DE, [Hyp.

And, AB coinciding with DE, AC will fall on DF, because the angle BAC is equal to the angle EDF. [Hypothesis.

Therefore also the point C will coincide with the point F, because AC is equal to DF. [Hypothesis.

But the point B was shewn to coincide with the point E, therefore the base BC will coincide with the base EF;

because, B coinciding with E and C with F, if the base BC does not coincide with the base EF, two straight lines will enclose a space; which is impossible. [Axiom 10.

Therefore the base BC coincides with the base EF, and is equal to it. [Axiom 8.

Therefore the whole triangle ABC coincides with the whole triangle DEF, and is equal to it. [Axiom 8.

And the other angles of the one coincide with the other angles of the other, and are equal to them, namely, the angle ABC to the angle DEF, and the angle ACB to the angle DFE.

Wherefore, if two triangles &c. q.e.d.

and join FC, GB.

PROPOSITION 5. THEOREM

The angles at the base of an isosceles triangle are equal to one another; and if the equal sides be produced the angles on the other side of the base shall be equal to one another.

Let ABC be an isosceles triangle, having the side AB equal to the side AC, and let the straight lines AB, AC be produced to D and E: the angle ABC shall be equal to the angle ACB, and the angle CBD to the angle BCE.

In BD take any point F,

and from AE the greater cut off AG equal to AF the less, [I.3.

Because AF is equal to AG [Constr.

and AB to AC, [Hypothesis.

the two sides FA, AC are equal to the two sides GA, AB, each to each; and they contain the angle FAG common to the two triangles AFC, AGB;

therefore the base FC is equal to the base GB, and the triangle AFC to the triangle AGB, and the remaining angles of the one to the remaining angles of the other, each to each, to which the equal sides are opposite, namely the angle ACF to the angle ABG, and the angle AFC to the angle AGB. [I. 4.

And because the whole AF is equal to the whole AG, of which the parts AB, AC are equal, [Hypothesis.

the remainder BF is equal to the remainder CG. [Axiom 3.

And FC was shewn to be equal to GB;

therefore the two sides BF, FC are equal to the two sides CG, GB, each to each;

and the angle BFC was shewn to be equal to the angle CGB; therefore the triangles BFC, CGB are equal, and their other angles are equal, each to each, to which the equal sides are opposite, namely the angle FBC to the angle GCB, and the angle BCF to the angle CBG. [I. 4.

And since it has been shewn that the whole angle ABG is equal to the whole angle ACF,

and that the parts of these, the angles CBG, BCF are also equal;

therefore the remaining angle ABC is equal to the remaining angle ACB, which are the angles at the base of the triangle ABC. [Axiom 3.

And it has also been shewn that the angle FBC is equal to the angle GCB, which are the angles on the other side of the base.

Wherefore, the angles &c. q.e.d.

Corollary. Hence every equilateral triangle is also equiangular.

PROPOSITION 6. THEOREM

If two angles of a triangle be equal to one another, the sides also which subtend, or are opposite to, the equal angles, shall be equal to one another.

Let ABC be a triangle, having the angle ABC equal to the angle ACB: the side AC shall be equal to the side AB.

For if AC be not equal to AB, one of them must be greater than the other.

Let AB be the greater, and from it cut off DB equal to AC the less, [I. 3.

and join DC.

Then, because in the triangles DBC, ACB, DB is equal to AC, [Construction.

and BC is common to both,

the two sides DB, BC are equal to the two sides AC, CB each to each;

and the angle DBC is equal to the angle ACB; [Hypothesis.

therefore the base DC is equal to the base AB, and the triangle DBC is equal to the triangle ACB, [I. 4.

the less to the greater; which is absurd. [Axiom 9.

Therefore AB is not unequal to AC, that is, it is equal to it.

Wherefore, if two angles &c. q.e.d.

Corollary. Hence every equiangular triangle is also equilateral.

PROPOSITION 7. THEOREM.

On the same base, and on the same side of it, there cannot be two triangles having their sides which are terminated at one extremity of the base equal to one another, and likewise those which are terminated at the other extremity equal to one another.

If it be possible, on the same base AB, and on the same side of it, let there be two triangles ACB, ADB, having their sides CA, DA, which are terminated at the extremity A of the base, equal

to one another, and likewise their sides CB, DB, which are terminated at B equal to one another.

Join CD. In the case in which the vertex of each triangle is without the other triangle;

because AC is equal to AD,[Hypothesis.

the angle ACD is equal to the angle ADC.[I. 5.

But the angle ACD is greater than the angle BCD,[Ax. 9.

therefore the angle ADC is also greater than the angle BCD;

much more then is the angle BDC greater than the angle BCD.

Again, because BC is equal to BD,[Hypothesis.

the angle BDC is equal to the angle BCD.[I. 5.

But it has been shewn to be greater; which is impossible.

But if one of the vertices as D, be within the other triangle ACB, produce AC, AD to E, F.

Then because AC is equal to AD, in the triangle ACD, [Hyp.

the angles ECD, FDC, on the other side of the base CD, are equal to one another. [I. 5.

But the angle ECD is greater than the angle BCD, [Axiom 9.

therefore the angle FDC is also greater than the angle BCD;

much more then is the angle BDC greater than the angle BCD.

Again, because BC is equal to BD, [Hypothesis.

the angle BDC is equal to the angle BCD. [I. 5.

But it has been shewn to be greater; which is impossible.

The case in which the vertex of one triangle is on a side of the other needs no demonstration.

Wherefore, on the same base &c. q.e.d.

PROPOSITION 8. THEOREM

If two triangles have two sides of the one equal to two sides of the other, each to each, and have likewise their

Full text

Wikisource:The_Elements_of_Euclid_for_the_Use_of_Schools_and_Colleges/Book_I.